Company
Interactive Demos
This demo deals with the determination of the coefficients of a chemical equation. These equations describe the interaction between chemical compounds/elements qualitatively, as well as quantitatively. Reactants are written on the left hand side, and products on the right hand side.
Examples
2 Na + Cl2 =
2 NaCl
C2H5OH +
3 O2 =
2 CO2 +
3 H2O
The number and type of atoms have to be identical on both sides of the equation. The so-called stoichiometric coefficients, which are highlighted in blue, in the above examples, ensure that the same number of atoms of an element is present on both sides of the equation. The determination of these coefficients is also called balancing of a chemical equation. Such equations are mainly used in inorganic chemistry, whereas organic chemistry resorts to structural formulas, when defining an equation. In the case of simple equations, the coefficients can be determined by trial and error, but when more complex equations are involved, this approach often turns out to be impractical.
Example for a complex equation3 As2S3 + 28 HNO3 + 4 H2O = 6 H3AsO4 + 9 H2SO4 + 28 NO
Solve stoichiometric equation
Handling
-
Input: In this field you can enter a chemical equation. Factors can be entered simply as
numbers - e.g. H20. The correct presentation of the input is simultaneously achieved in the Equation field, which
displays the factors of the elements as subscripts. The current version does not support ionic equations.
A valid equation must meet the following criteria:- Have the same elements on both sides of the equation.
-
Elements are be represented by their international symbols (IUPAC-nomenclature):
from H Hydrogen to U Uranium - Valid operators: + = ( ) [ ] { } Comment: The number of opening and closing parentheses must be identical!
- Equation: This field presents the equation without coefficients.
- Result: This field presents the equation with the coefficients determined or the corresponding error message.
Mathematical background
This servlet applies the Gaussian elimination method to determine the unknown coefficients of a chemical equation.
The following example may serve as an explanation: The introduction of chlorine into hot potash lye will lead to the following reaction products: potassium chlorate, potassium chloride and water.
x1 KOH + x2 Cl2 = x3 KClO3 + x4 KCl + x5 H2O
The above leads to the following connection for the number of K,O, H and Cl-atoms:
|
x1 =
x3 +
x4
x1 = 3x3 + x5 x1 = 2x5 2x2 = x3 + x4 |
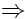
|
x1 -
x3 -
x4 =
0
x1 - 3x3 = x5 x1 = 2x5 2x2 - x3 - x4 = 0 |
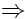
|
1 0 -1 -1 0
1 0 -3 0 1 1 0 0 0 2 0 2 -1 -1 0 |
One step of the Gaussian elimination method is to transfer this matrix into the so-called reduced row echelon form by means of the following transformations:
This equation can be transformed as follows:- if you switch two rows of the matrix.
- if you multiply one row by a non-zero number.
- if you multiply one row by a factor and add the multiple to another row of the matrix.
The operations i.-iii. result in the following reduced row echelon form of the matrix
1 0 0 0 2
0 2 -1 -1 0
0 0 -3 0 -1
0 0 0 3 5
The last step is to determine the coefficients of the equation by means of the so-called back substitution; here only integral coefficients are relevant. Thus, the solution is as follows:
|
x1 = 6
x2 = 3
x3 = 1
x4 = 5
x5 = 3
|
implies |
6 KOH +
3 Cl2 =
KClO3 +
5 KCl +
3 H2O
|